Notice
Recent Posts
Recent Comments
Link
Star_project
카이제곱 검정 - 독립성검정 in python 본문
참고 도서 : https://www.aladin.co.kr/shop/wproduct.aspx?ItemId=287310138
경영경제 통계학
4차 산업혁명 시대의 주역은 통계학, 수학에서 다루는 개념을 제대로 이해하고 이를 실제 데이터 분석에 잘 활용할 수 있는 사람이라 할 수 있다. 대학에서 처음으로 통계학을 접하는 경제·경영
www.aladin.co.kr
1. 독립 여부에 대한 카이제곱 검정
# 규정의 위치 X 웹사이트 국적 분할표 (웹페이지 빈도)
import pandas as pd
df = pd.DataFrame({'프랑스':[56, 19, 6, 12],
'영국':[68, 19, 10, 9],
'미국': [35,28, 16, 13]},
index=['홈페이지', '주문페이지', '고객정보 페이지', '기타 페이지'])
df1. 독립 여부에 대한 카이제곱 검정
- 분할표는 n개의 관측치를 여러 범주로 나누어 교차분석표 형태로 나타낸 것을 말한다. 표의 각 셀은 그 셀의 행과 열로 정의되는 범주에 속하는 관측치 개수를 나타낸다.

'''
카이제곱 검정
r x C 분할표에서 독립 여부에 대한 가설검정은 다음과 같다.
* H0 : 변수 A는 변수 B와 서로 독립이다.
* H1 : 변수 A와 변수 B는 서로 독립이 아니다.
- 분할표에서 변수 A와 B의 관련성 정도를 측정한다. 카이제곱 검정에서 수행하는 연산은 오직 n개의 데이터 쌍을 r개의 행(변수 A)와 c개의 열(변수 B)로 분류한 후 분할표의 각 셀에 있는 관측빈도수와 독립이라는 가정하에서 계산한 예상빈도수를 서료 비교하는 것이다. 카이제곱 검정통계량은 다음과 같이 예상빈도수와 관측빈도수의 상대적인 차이를 측정한다.
- 서로 독립이면 0에가까움.
- 항상 제곱을하기 때문에 음수 없음. 그래서 우측검정을 사용함.
'''
1단계 : 가설 설정
2단계 : 결정규칙 설정
3단계 : 검정통계량 계산
4단계 : 기각여부 결정

1단계 : 가설 설정
2단계 : 결정규칙 설정
'''
카이제곱 계산 예시
**1단계 : 가설 설정**
- H0 = 개인정보 보호 규정 위치는 웹페이지의 국적과 무관하다.
- H1 = 개인정보 보호 규정 위치는 웹페이지의 국적에 따라 달라진다.
**2단계 : 결정규칙 설정**
- 자유도는 (4-1)(3-1) = 6
- 가설검정을 위해 alpha = 0.05 를 선택. 우측검정 임계치로 보면 chi2 0.05 = 12.59
- chi2calc > 12.59 이면 귀무가설 H0를 기각하고 그렇지않으면 기각할 수 없다.
'''3단계 : 검정통계량 계산
# 3단계 검정통계량 계산
import scipy.stats as stats
stats.chi2_contingency(observed = df)결과
(17.543931463609706,
0.007478972103908569,
6,
array([[50.81443299, 57.91752577, 50.26804124],
[21.09278351, 24.04123711, 20.86597938],
[10.22680412, 11.65635739, 10.11683849],
[10.86597938, 12.38487973, 10.74914089]]))# 독립성 검정 실시
chi, pvalue, dof, expected = stats.chi2_contingency(df, correction=False)
# 기댓값 출력
pd.DataFrame(data=expected, columns=df.columns, index=df.index)결과

# 유의수준, 자유도로 검정통계량 구하기
stats.chi2.ppf(0.95, 6)결과
12.5915872437439774단계 : 기각여부 결정
'''
**4단계 : 기각여부 결정**
- 카이제곱값 = 17.54 는 12.59 초과하기 때문에 우리는 예상빈도수와 관측빈도수 간 차이가 유의수준 5%에서
유의함을 알 수 있다.
- p값(0.0075)은 귀무가설이 기각되어야 함을 보여준다.
- 유의수준 alpha = 0.05 하에서 291개 웹사이트 표본에 근거할 때 p값은 개인정보 보호규정 위치는
웹페이지의 국적과 서로 독립이 아님을 의미한다.
'''
**교차분석표**
- 독립여부에 대한 카이제곱 검정은 매우 유연한 형태를 가진다. 대부분 성별(남성, 여성)과 같은 범주형 변수와 함께 사용되지만, 정량적 변수(예:월급)를 범주(구간으로나누기)로 코딩한 후에 역시 카이제곱 검정을 실시할 수 있다.
연습문제)
미국이 각 주에 대해 X = 인구 100,000명당 의사 수이고 Y = 신생아 1,000명 중 영아 사망수이다. 우리는 인구에 비해 의사가 많은 주에서 영아 사망 수가 낮다는 가설을 세울 수 있지만 정말 그러한가? 정규분호와 등분산을 가정하지 않았기 때문에 t검정을 원하지 않는다. 대신 우리는 다음과 같은 가설을 설정하였다.
- H0 : 영아 사망률은 인구 100,000명당 의사 수와 독립적이다.
- H1 : 영아 사망률은 인구 100,000명당 의사 수와 독립적이지 않다.
## 1,000명 출산당 영아사망률 X 인구 100,000audekd dmltk tn
df = pd.DataFrame({'낮음':[4, 5, 8],
'중간':[6, 6, 5],
'높음': [6, 6, 4]},
index=['낮음', '중간', '높음'])
df
stats.chi2_contingency(observed = df)(2.100454152249135, 0.7172889504963147, 4, array([[5.44, 5.44, 5.12],
[5.78, 5.78, 5.44],
[5.78, 5.78, 5.44]]))p값(0.7173)으로부터 우리는 의사 수와 영아 사망률과는 강한 관계가 없는 것이라고 결론을 내린다.
**단원 연습문제**
(a) 가설을 설정해라.
(b) 각 분할표의 자유도를 어떻게 계산하는가?
(C) 주어진 유의수준에서 임계치를 구하라.
(d) 독립 여부에 대한 카이제곱 검정을 실시하고 결론을 제시하라.
(e) 분할표의 어떤 셀이 카이제곱 검정통계량에 가장 크게 기여하는가?
(f) 예상빈도수가 매우 작은 값이 있는가?
(g) p값을 해석하라.
예제1
# 예제1
# 캘리포니아 거주자 중에 최근 자동차 판매점을 방문한 사람을 무작위로 추출하여 어떤 유형의 차량을 구매할 가능성이 높은지 조사하였다. 결과는 다음 표에 제시되어 있다. 유의주순 10%에서 차량 유형 선택은 구매자의 연령과 무관한가?
# 차량유형(행) X 구매자의 연령(열)
df = pd.DataFrame({'30미만':[5, 15, 25, 15],
'30에서50사이':[10, 30, 25, 15],
'50이상': [15, 45, 25, 15]},
index=['디젤', '가솔린', '하이브리드', '전기'])
df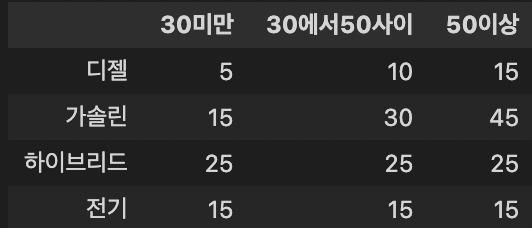
chi2, p, dof, expected = stats.chi2_contingency(observed = df)
result = 'Test Statistic: {}\np-value: {}\nDegree of Freedom: {}'
print(result.format(chi2, p, dof))
print(expected)결과
Test Statistic: 10.666666666666668
p-value: 0.09924119431764619
Degree of Freedom: 6
[[ 7.5 10. 12.5 ]
[22.5 30. 37.5 ]
[18.75 25. 31.25]
[11.25 15. 18.75]]# 유의수준, 자유도로 검정통계량 구하기
stats.chi2.ppf(0.99, 6)결과
16.811893829770927
답)
a. H0 : 차량유형과 구매자의 연령은 서로 독립이다.
b. 자유도 = (r-1)(c-1) = (4-1)(3-1)=6
c. stats.chi2.ppf(0.90, 6) = 16.81
d. = 검정통계량 10.667(p값 = 0.0992). 따라서 유의수준 10%에서 귀무가설을 기각한다.
e. '가솔린'과 '30미만'범주가 가장 크게 기여한다.
f. 각 셀의 예측빈도는 5보다 크다.
g. p 값은 유의수준에 가깝지만 유의수준보다는 작기 때문에 귀무가설을 기각한다.
예제2
# 예제2
# MBA 프로그램에 지원한 학생들은 반드시 언어와 수리영역 GMAT 점수를 제출하여야 한다.
# 미국 중서부에 위치한 AACSB 인증을 받은 공립 경영대학에서 무작위로 뽑은 MBA 지원자 100명의 점수가 아래와 같다.
# 유의수준 0.5%에서 수리점수는 언어점수와 무관한가?
# 언어점수(행) X 수리점수(열)
df = pd.DataFrame({'25점이하':[25, 4, 1],
'25~34점':[9,28, 3],
'35점이상': [1, 18, 11]},
index=['25점이하', '25~34점', '35점이상'])
df
chi2, p, dof, expected = stats.chi2_contingency(observed = df)
result = 'Test Statistic: {}\np-value: {}\nDegree of Freedom: {}'
print(result.format(chi2, p, dof))
print(expected)결과
Test Statistic: 55.88253968253969
p-value: 2.12216072663507e-11
Degree of Freedom: 4
[[10.5 14. 10.5]
[15. 20. 15. ]
[ 4.5 6. 4.5]]# 유의수준, 자유도로 검정통계량 구하기
stats.chi2.ppf(0.995, 4)결과
14.860259000560243답)
a. $H$<sub>0</sub>:'언어점수' 와 '수리점수'변수는 서로 독립이다.
b. 자유도 = (r-1)(c-1) = (4-1)(3-1)=4.
c. stats.chi2.ppf(0.995, 4) = 14.86.
d. = 검정통계량 55.88(p값 = 0.0000). 따라서 유의수준 0.5%에서 귀무가설을 기각한다.
e. '25점 이하'(수리점수) '25점이하'(언어점수) 범주가 가장 크게 기여한다.
f. 각 셀의 예측빈도는 5보다 작다.
g. p 값은 거의 0에 가깝다. (관찰된 차이가 우연은 아니다.)
예제3
# 예제3
# 마케팅 연구자들은 설문조사를 수행하기 전에 이를 미리 공지하고 연구의 목적을 설명하는 이메일을 발송하였다. 대상 고객들의 50%는 이와 같은 이메일을 받았고, 나머지 50%는 그런 절자없이 바로 설문조사를 실시하였다. 설문조사의 응답률은 아래와 같다.
# 유의수준 2.5%에서 응답률은 사전 공지 이메일과 무관한가?
# 공지여부(행) X 공지여부와 반응률에 대한 교차분석표(열)
df = pd.DataFrame({'반응':[39, 22],
'무반응':[155, 170]},
index=['미리 공지', '미리 공지하지 않음'])
df
chi2, p, dof, expected = stats.chi2_contingency(observed = df)
result = 'Test Statistic: {}\np-value: {}\nDegree of Freedom: {}'
print(result.format(chi2, p, dof))
print(expected)결과
Test Statistic: 4.78956412260631
p-value: 0.028632671425217433
Degree of Freedom: 1
[[ 30.65803109 163.34196891]
[ 30.34196891 161.65803109]]# 유의수준, 자유도로 검정통계량 구하기
stats.chi2.ppf(0.975, 1)결과
5.023886187314888답)
a. H0: 반응률과 사전공지 이메일 변수는 서로 독립이다.
b. 자유도 = (r-1)(c-1) = (4-1)(3-1)=1.
c. stats.chi2.ppf(0.975, 1) =5.024
d. = 검정통계량 5.42(p값 = 0.0199). 따라서 유의수준 2.5%에서 귀무가설을 기각한다.
e. '반응'과 '미리 공지하지 않음'범주가 가장 크게 기여한다.
f. 각 셀의 예측빈도는 5보다 크다.
g. p 값은 0.025 보다 작다.(관찰된 차이가 우연은 아니다.)
* 피셔의정합검정
# 빈도수가 5 이하가 있을 경우 피셔의 정합검정 사용함.
data = pd.DataFrame([[1, 6], [5, 2]])
data.columns = ['가짜 약','진짜 약']
data.index = ['효과있음', '효과없음']
data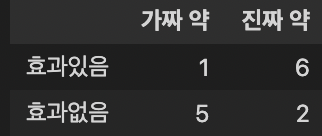
oddsratio, pvalue = stats.fisher_exact(data)
print("oddratio:", oddsratio, "\n"
"p-value:", pvalue )
# 이때 주로 p 값으로 결과 해석oddratio: 0.06666666666666667
p-value: 0.10256410256410275
